演算光线的偏折，《张朝阳的物理课》走进天文馆讲解光的运动方程

展开全文

这一方法的预测结论是牛顿理论的两倍，与爱丁顿实验对日食观测的结果严格一致，并在现代天文学中通过引力透镜效应、黑洞视界阴影、黑洞光子球等精确观测中被不断证实。因此，从理论本质、物理严谨性和计算精度而言，广义相对论无疑是描述光线偏折现象最深入、最全面、最准确的理论框架。

（张朝阳讲解计算光线偏折的不同路径)

测地线与测地线方程

在广义相对论中，“引力”并不真实存在，一个只受引力作用的物体在时空中会走“直线”。无论物体的质量有多少，下落的轨迹都是相同的。没有一个像是牛顿第二定律中的力F在影响着物体运动，所谓“引力”只是时空背景的改变，而无论背景如何，不受其它力的物体要做惯性运动。这体现了爱因斯坦对引力质量和惯性质量的深刻洞见，这两种质量就是完全相同的！

弯曲时空有自己的“直线”也就是测地线。测地线是一类特殊的曲线，其本质特征表现为切矢的自平移性。具体而言，当选择曲线参数为仿射参数后，在测地线上任意一点处的切矢，如果沿着测地线自身进行平行输运（parallel transport），也即不额外引入任何“转动”或“加速度”，则输运后的切矢仍与该点处的切矢方向完全相同。

换句话说，测地线上的切矢始终能通过曲线上的自平移保持平行，不产生额外的方向改变。这里给出一个非测地线与测地线对比的例子：在地球表面上，从北京飞往纽约可以有很多种航道，例如经过太平洋上空或经过北冰洋上空，北冰洋航线时间更短，假如严格在走球面大圆的一段就是测地线，而太平洋航线就是非测地线。在平直空间中，这种自平移的特性恰好由直线体现：直线上任一点的切矢经沿自身输运，始终保持方向不变。

因此，测地线可看作是弯曲空间中的“广义直线”，即直线概念向弯曲空间的自然推广。平直空间中两点之间线段最短，而广义相对论断言：光线在时空中沿类光测地线传播，本质上是在弯曲时空的几何结构中选取了自然的、最短或极值长度路径。

所以在广义相对论中讨论物体的运动，最重要的就是对测地线的描述，了解了测地线就能得到物体的运动方程。在此之前还有一步准备工作，也是必要前提，就是描述时空长什么样。爱因斯坦方程决定了时空的几何，也就是度规，光线偏折涉及的是太阳外部的时空，之前的课程已经对此有详细的讨论和计算，这里就不加证明的认为时空背景是史瓦西度规：

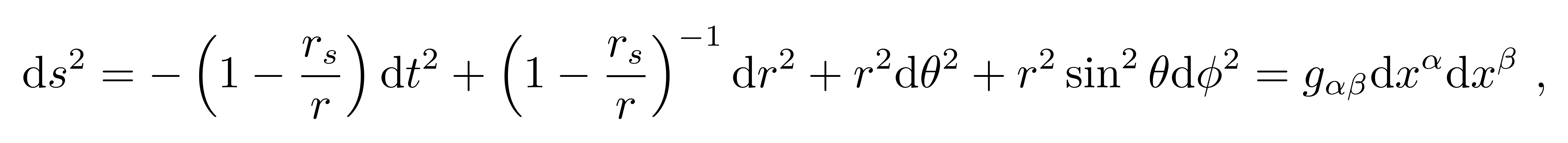
其中史瓦西半径

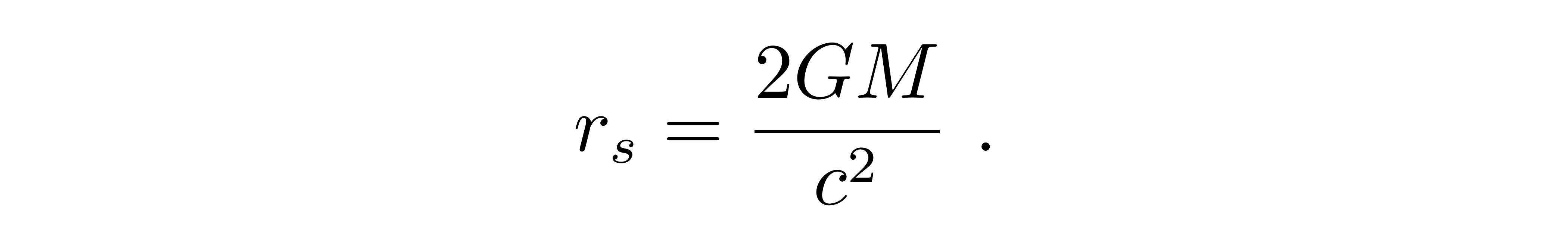
在广义相对论的处理中，也可以将光看作一种粒子即“光子”（并不必与量子论中的“光量子”完全对应），它的时空坐标为：

任意的一个一阶张量在时空中的平行移动以下式来表达：

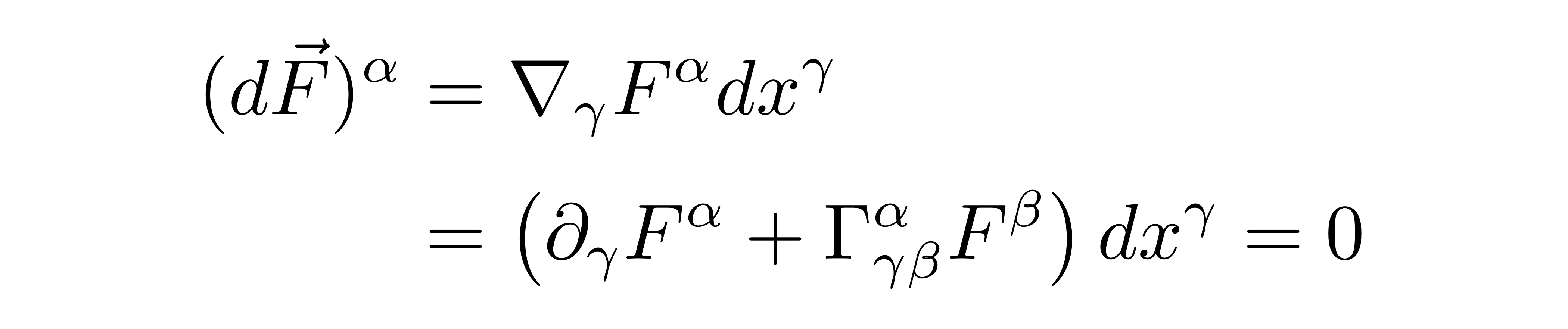
当这个一阶张量就是类时运动的粒子的四速度时有：

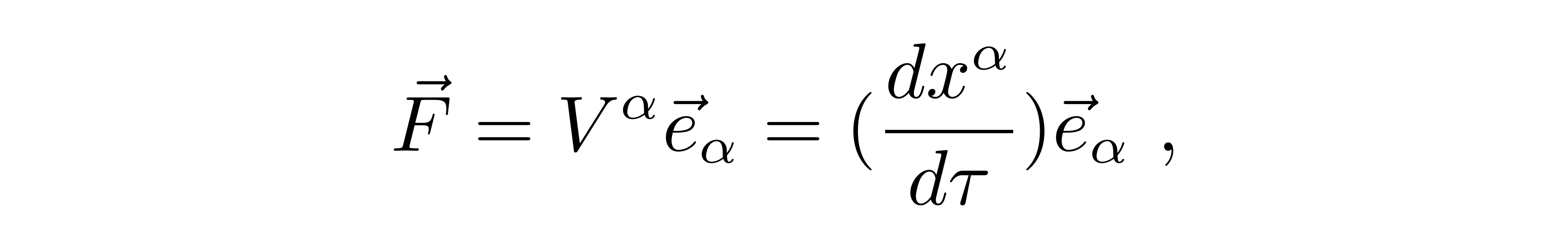
dτ是粒子的线长。然而对于类光的粒子而言，它的时空间隔恒为零，属于类光间隔

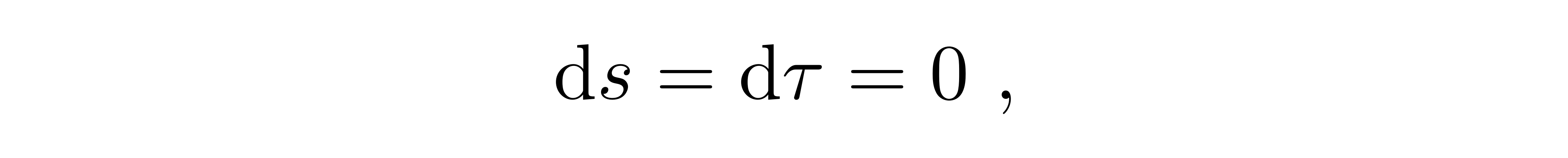
这使得类光粒子的原时间隔不能出现在分母上。之前已经提到，只有以仿射参数参数化的测地线切矢才是自平移的，对于类时测地线而言，线长参数自动是仿射参数，所以只要对类光测地线选择合适的参数成为仿射参数即可良好定义切矢的平行输运。找到仿射参数是总可以做到的，直观的看是因为类光粒子的传播是真实的物理事件。能够描述光的运动、它的演化、传播的参数λ就是类光测地线的仿射参数，λ当然是一个标量，也即：

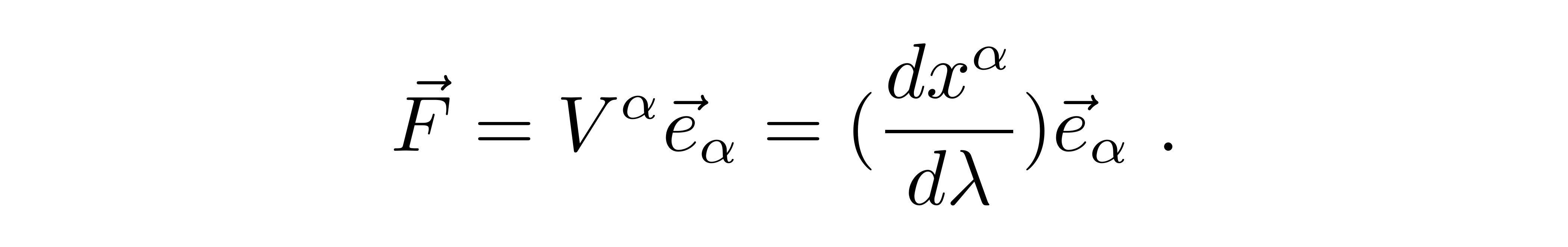
此时就得到了非常重要的类光测地线方程

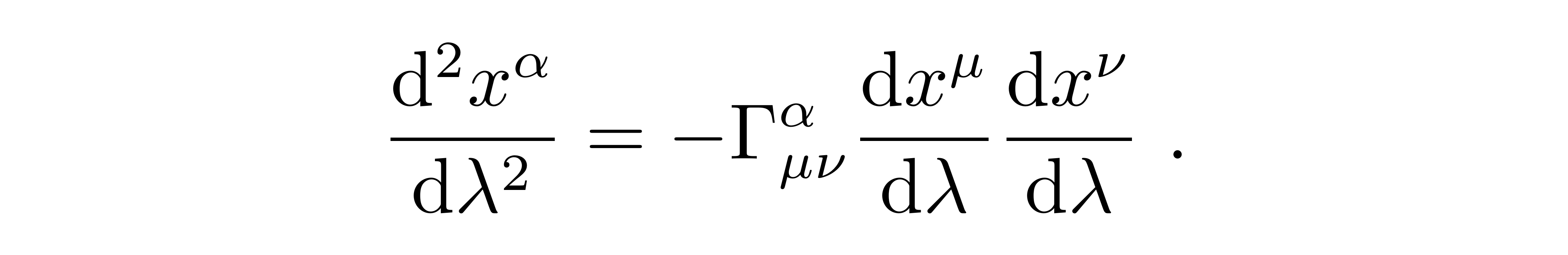
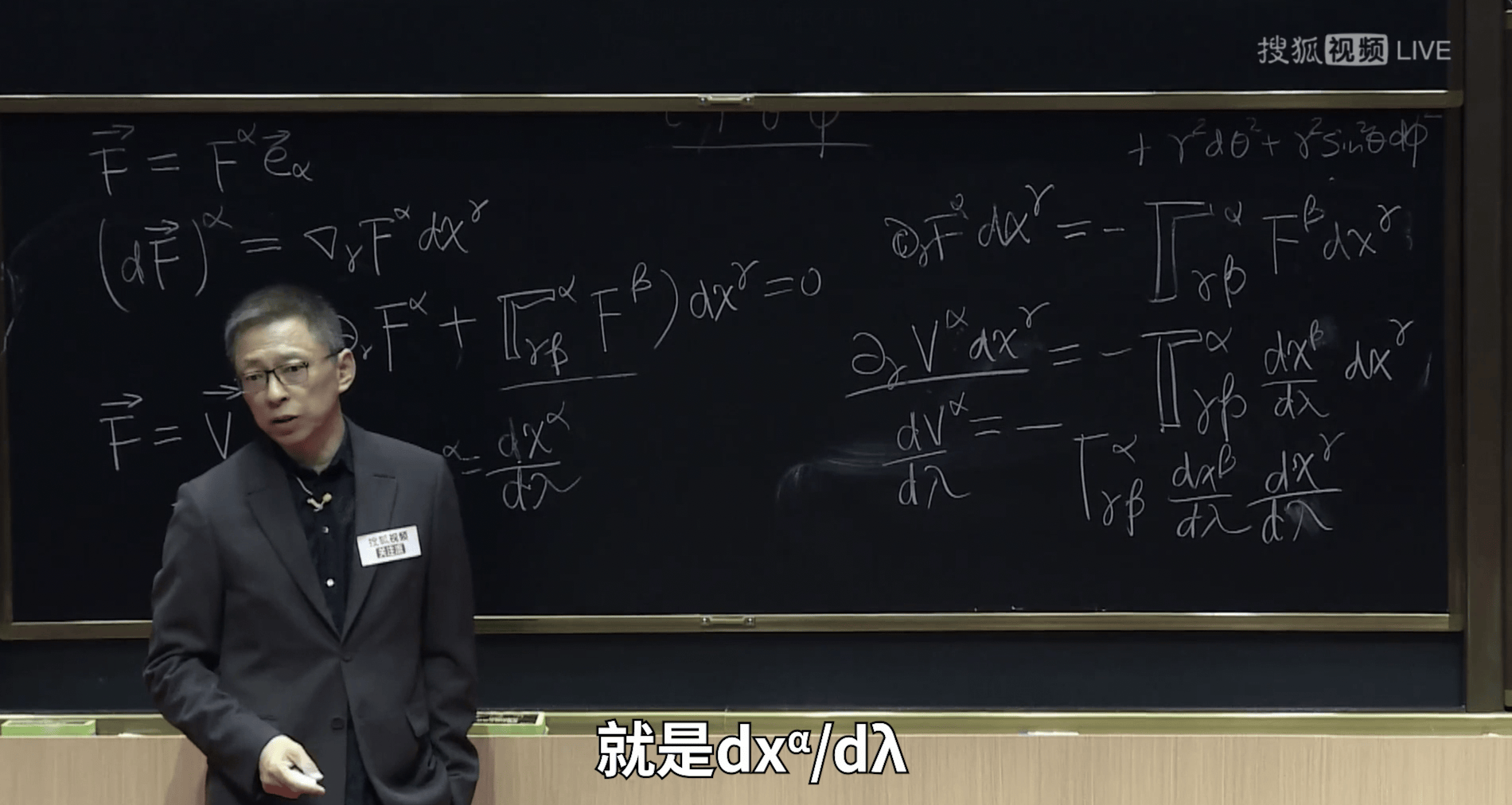（张朝阳用仿射参数写出光的测地线方程）

运用测地线方程，推导光的轨道方程

接下来就是将史瓦西度规代入到测地线方程来做具体的计算。当α=0时非0的克氏符只有：

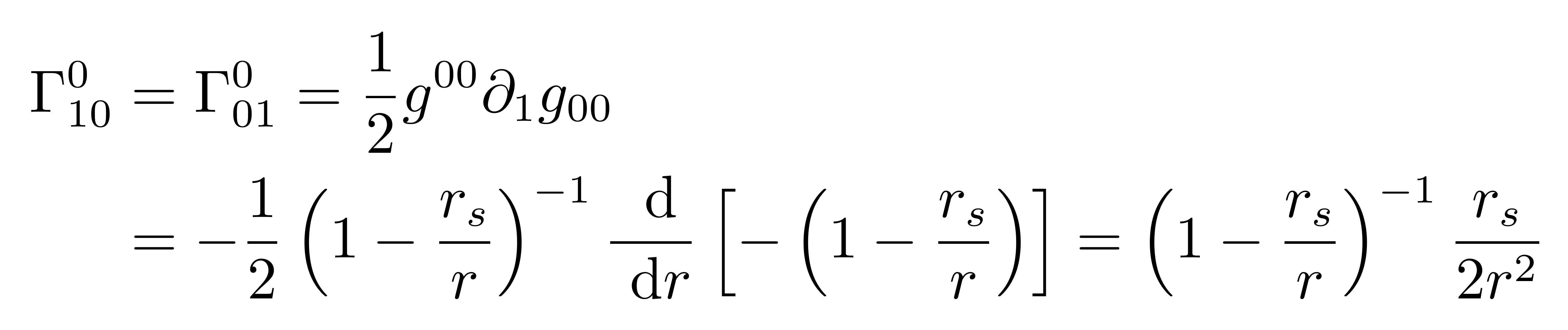
从而有关于坐标t的方程为：

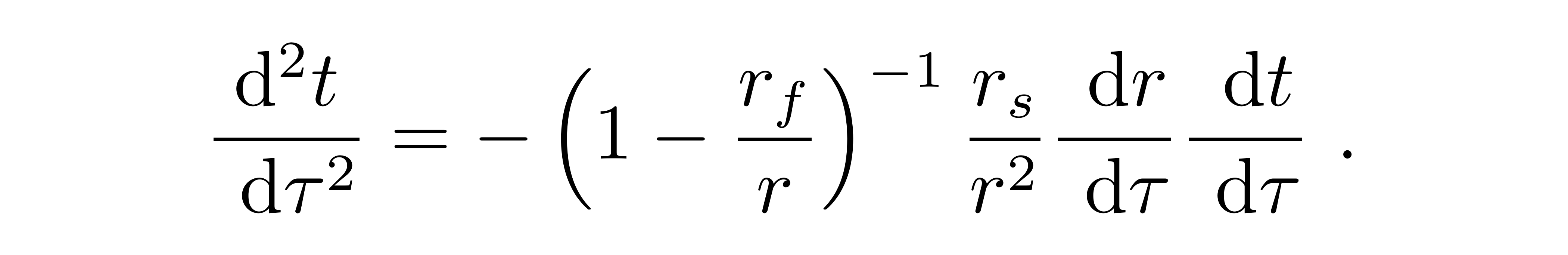
引入变量：

则微分方程变为：

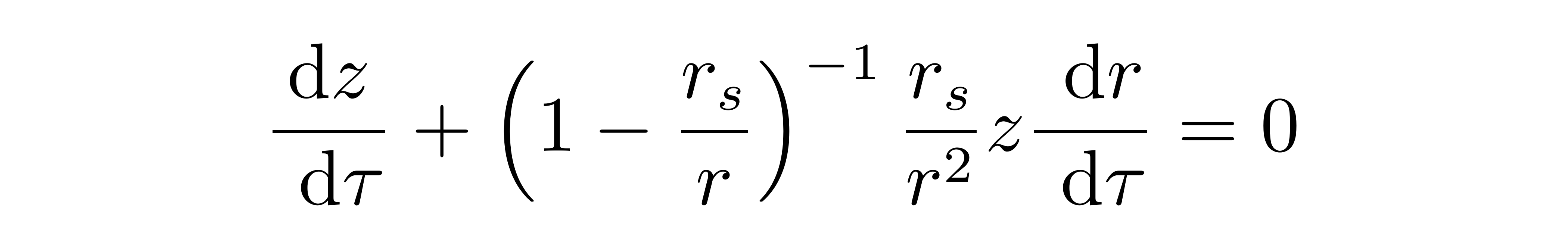
积分解得：

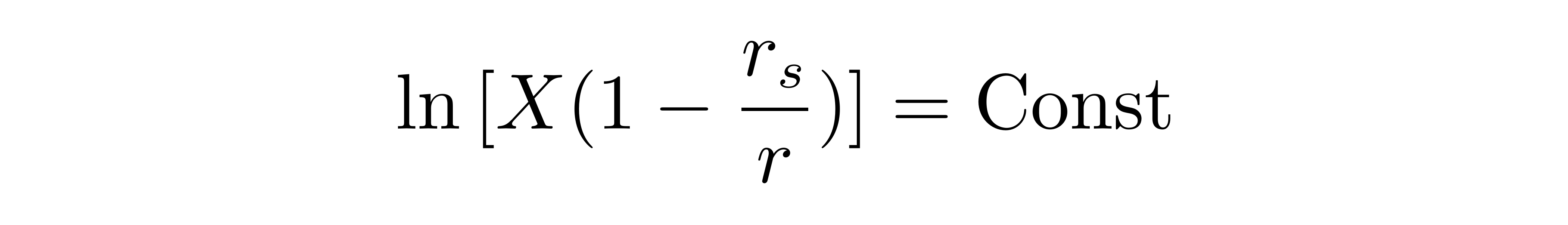
则最终方程的形式为：

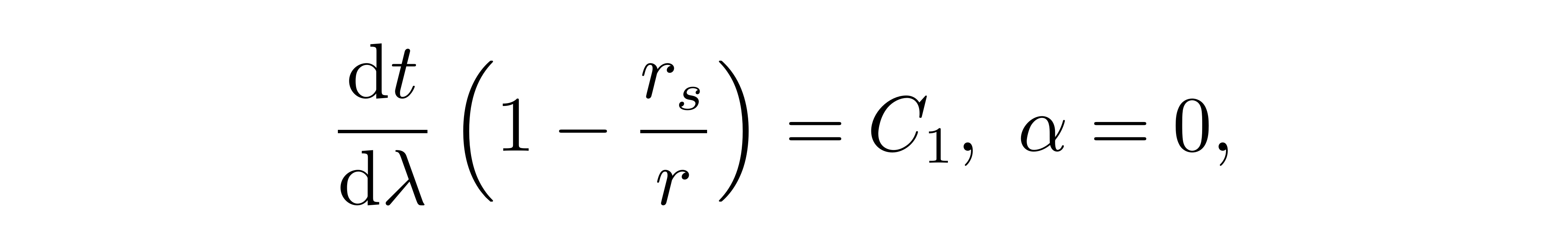
当α=3时，按照类似的分析，此时非0的克氏符只有：

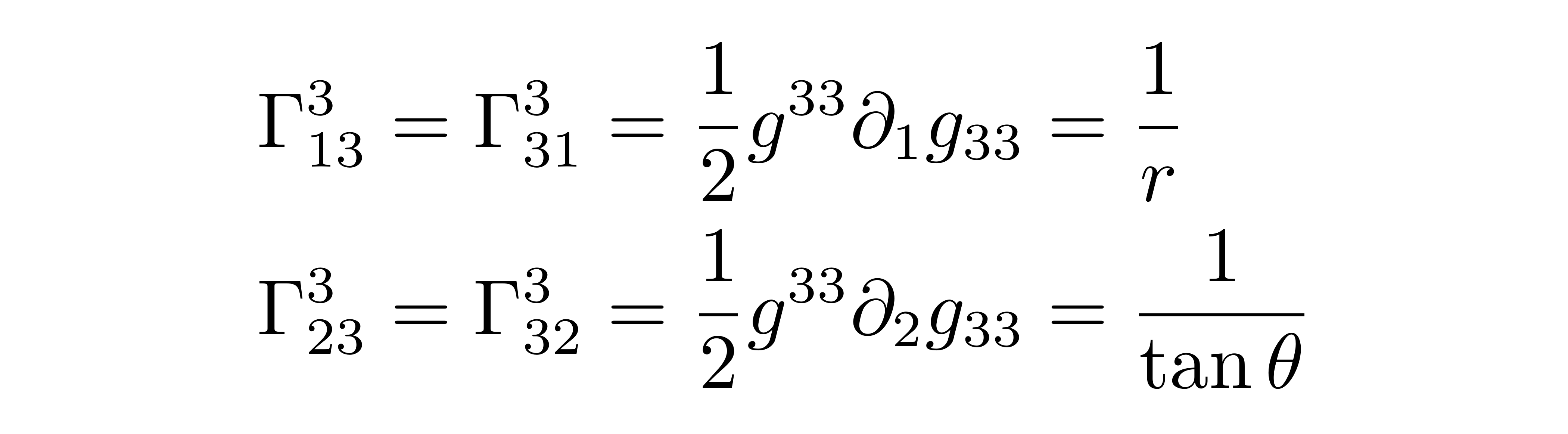
带入解出方位角Φ的方程为：

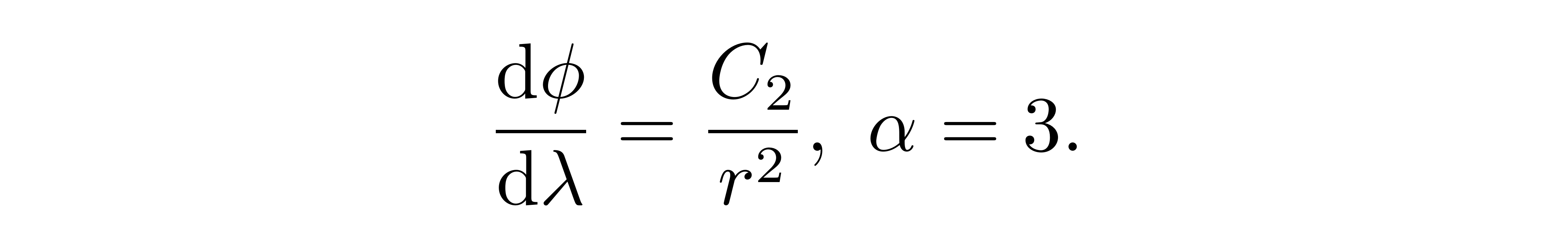
这里的两个方程的积分常数分别具有能量与角动量的含义，粗略的说，这对应了能量守恒与角动量守恒。正是因为有角动量守恒，光的运动将始终保持在等θ面上，这样我们总可以选取坐标系的极轴，把光的运动限制在赤道面上，对于α=2的分量这就是：

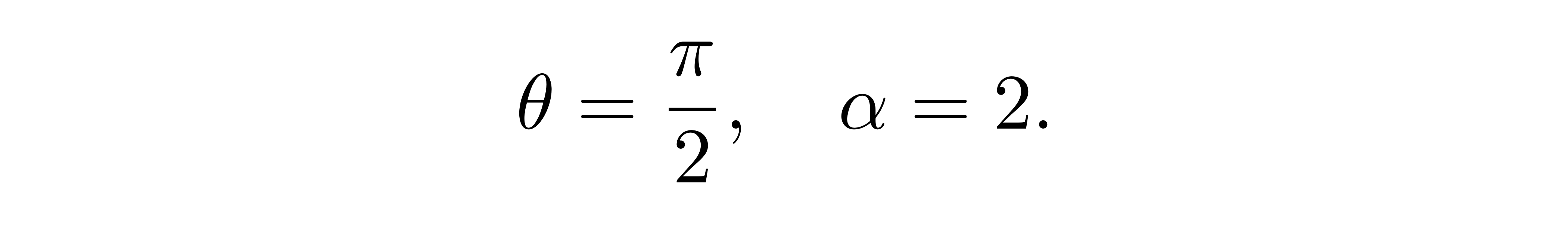
对于α=1分量，则不用硬代入测地线方程，而是用光的世界线线元为0的性质

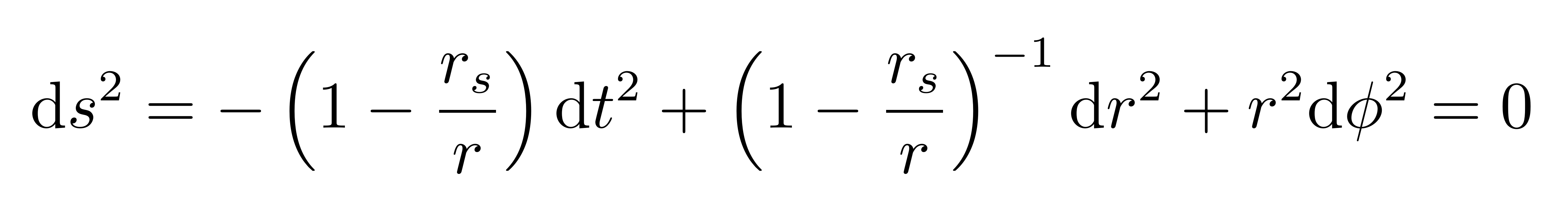
得到

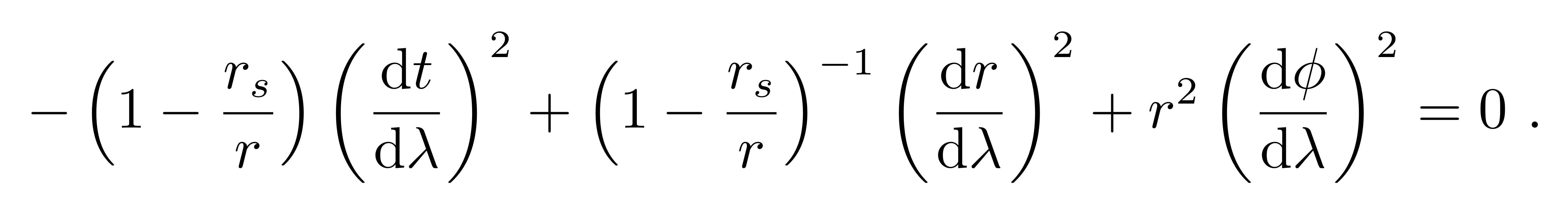
代入刚刚得到的α=0和3所对应的守恒量（积分常数）

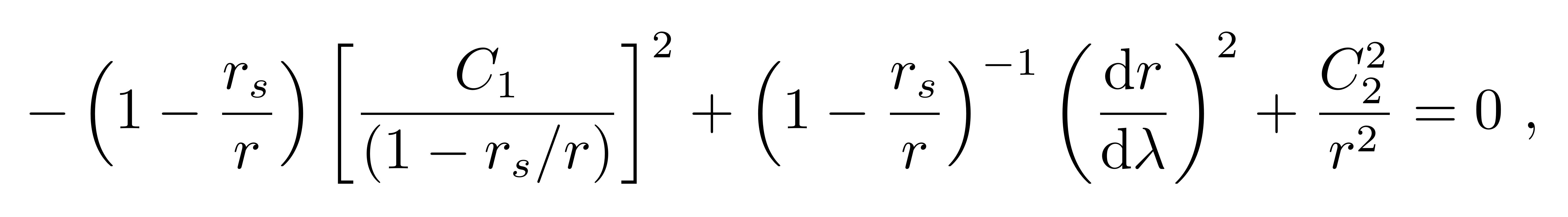
整理一下得到

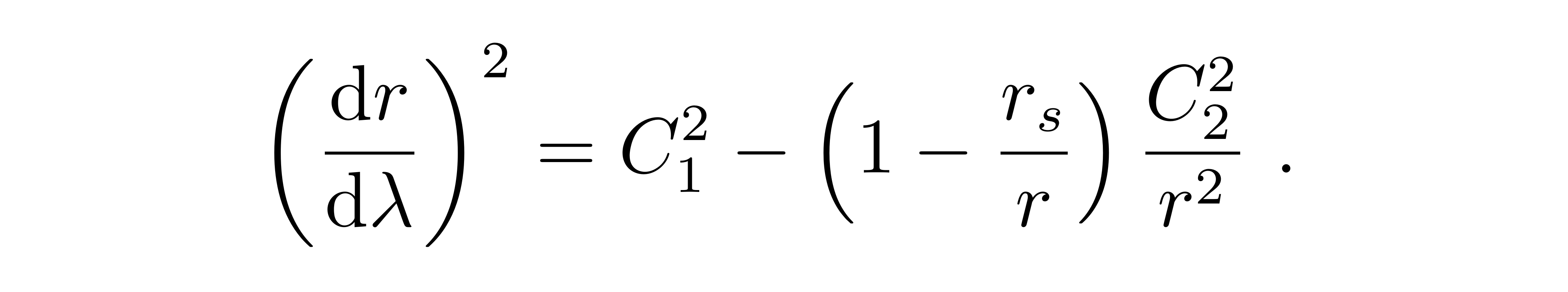
要求解的是r和Φ的关系，λ在这里只是起到一个中间参量的作用。为了突出待求解的r和Φ的关系，做变量替换

到这一步，就已经把和仿射参量λ有关的项统一用守恒量替换掉了。接下来仿照牛顿引力下行星运动轨迹的求解套路，对方程再做一次比耐代换，令y=1/r，得到：

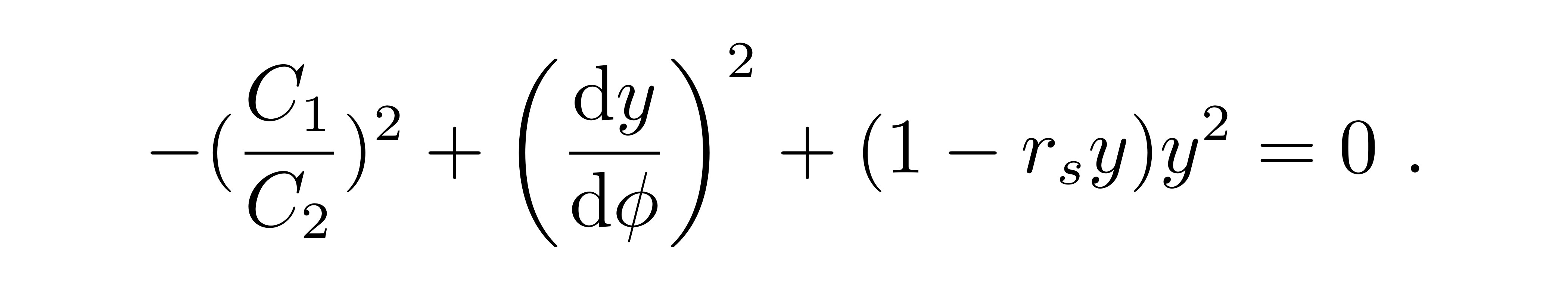
这是一个一阶微分方程，一阶项y’=dy/dΦ带有一个平方，可以方便地转化为类似牛顿引力情形的二阶微分方程，只需要两边同时再对Φ求导

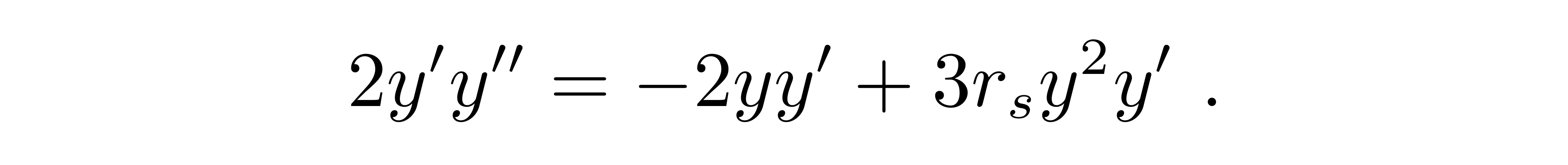
整理后，得到最终的轨道方程

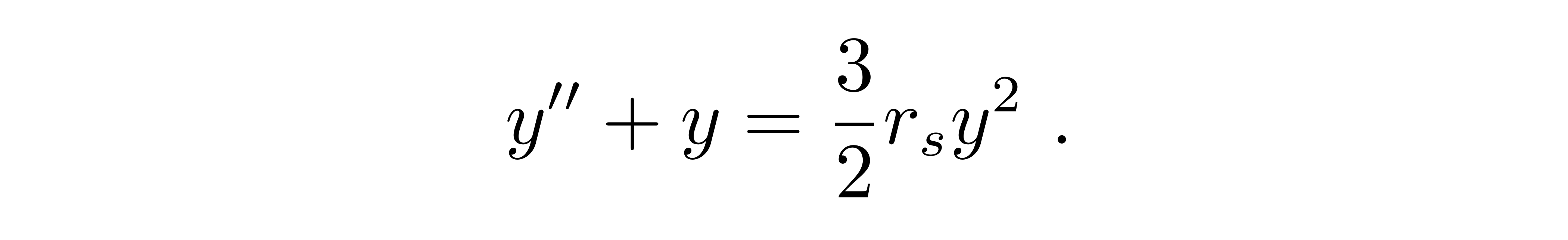
（张朝阳计算光的轨道方程）

用微扰近似求解轨道方程

现在来看看这个方程该如何求解。由于方程右侧出现了y的平方项，它不再是一个线性方程，难以严格求解。但本文所考虑的偏折光线的天体是太阳，对它而言，史瓦西半径大约是3km，而太阳本身的半径就有7×10⁵km。在光线经过太阳时，离太阳的距离更是要大于这个半径。这时就能够使用微扰法来试探求方程的近似解。可以认为方程右侧的平方项相比于y是一个小量

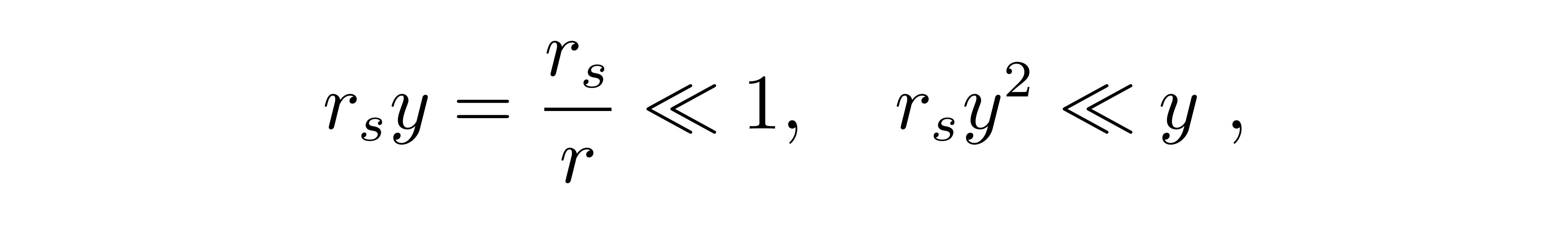
这样初步来看，方程的解应该很接近下面这个零级近似方程的解

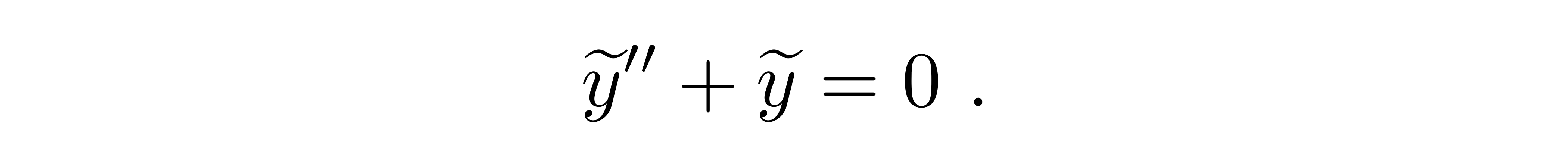
这个方程就是谐振子方程，它的解可以一眼看出。如果选取Φ=0对应光子从无穷远处入射而来的方向，方程的解就是

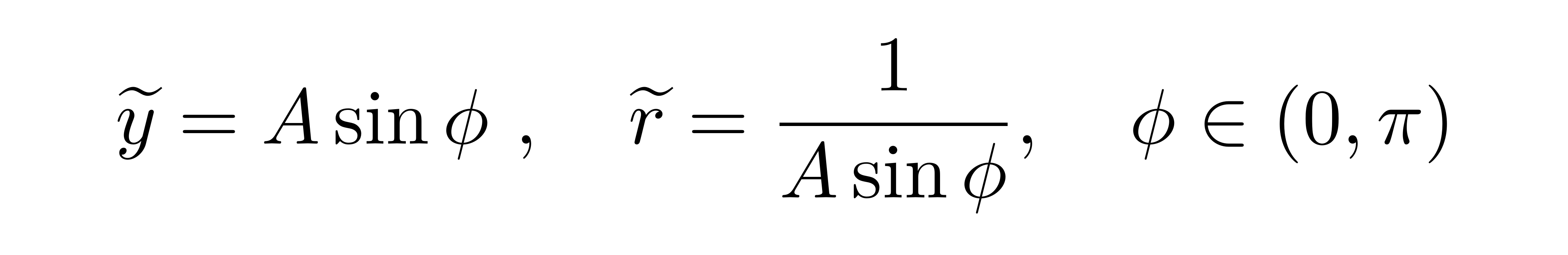
这是一个直线在极坐标系下的方程，意味着光线完全不被偏折。其中参数A代表直线离原点的距离的倒数。下面重新考虑刚刚被忽略掉的小量，类比微扰论的思想，把这个小量当做对近似方程的微扰，用零级近似解的三角函数形式作为对原方程一级近似解的试探函数。首先，把零级近似解代入到轨道方程右侧的小量中，

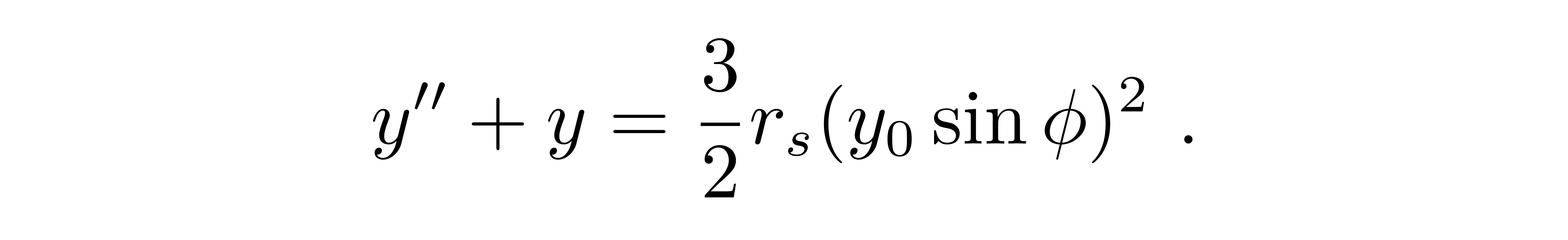
这里出现了三角函数的平方项，所以在一级近似解中，也应该展开到三角函数的平方项。根据这样的考虑，一级近似解的试探函数可以写为

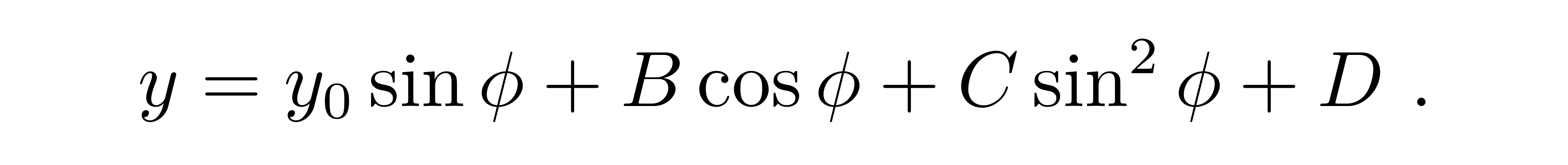
在上式中，之所以不包含cos²Φ，是因为它可以变换为1-sin²Φ，从而被吸收到第三项和第四项中。

接下来要考虑的是四个待定系数之间的关系。对于初始条件，仍然选取Φ=0对应光子无穷远的位置，这就要求

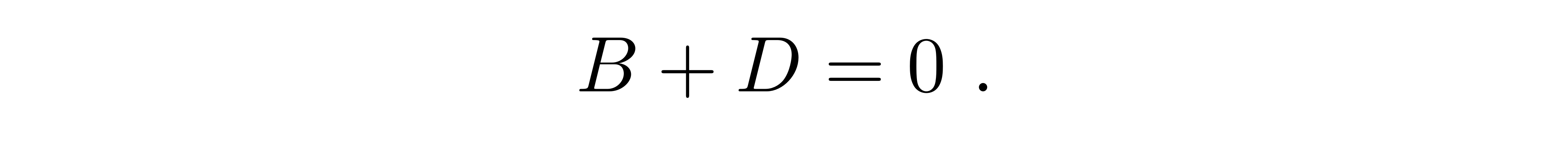
把一级近似的试探函数代入轨道方程的左侧，至于轨道方程的右侧，它是一个小量，所以仍然只代入零级近似解

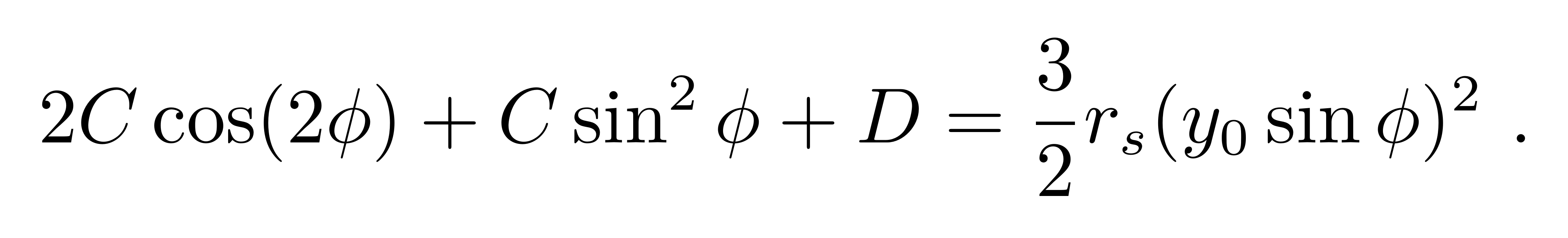
利用倍角关系，可以把三角函数中角度变量含有2的倍数的项统一成平方项，得到

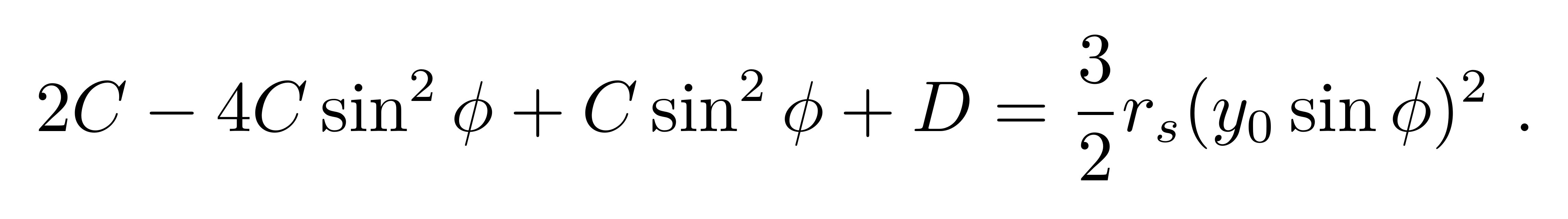
等式两边要对任意的Φ恒成立，就要求

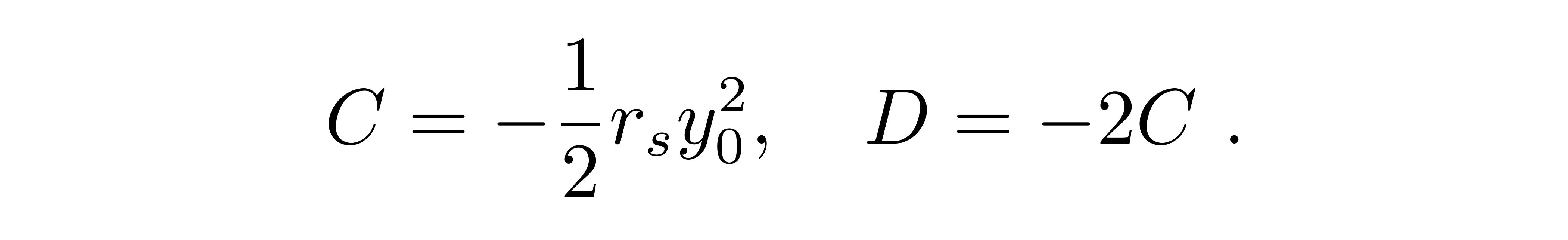
综合所得到的三个关系式，可以把一级近似试探解写成

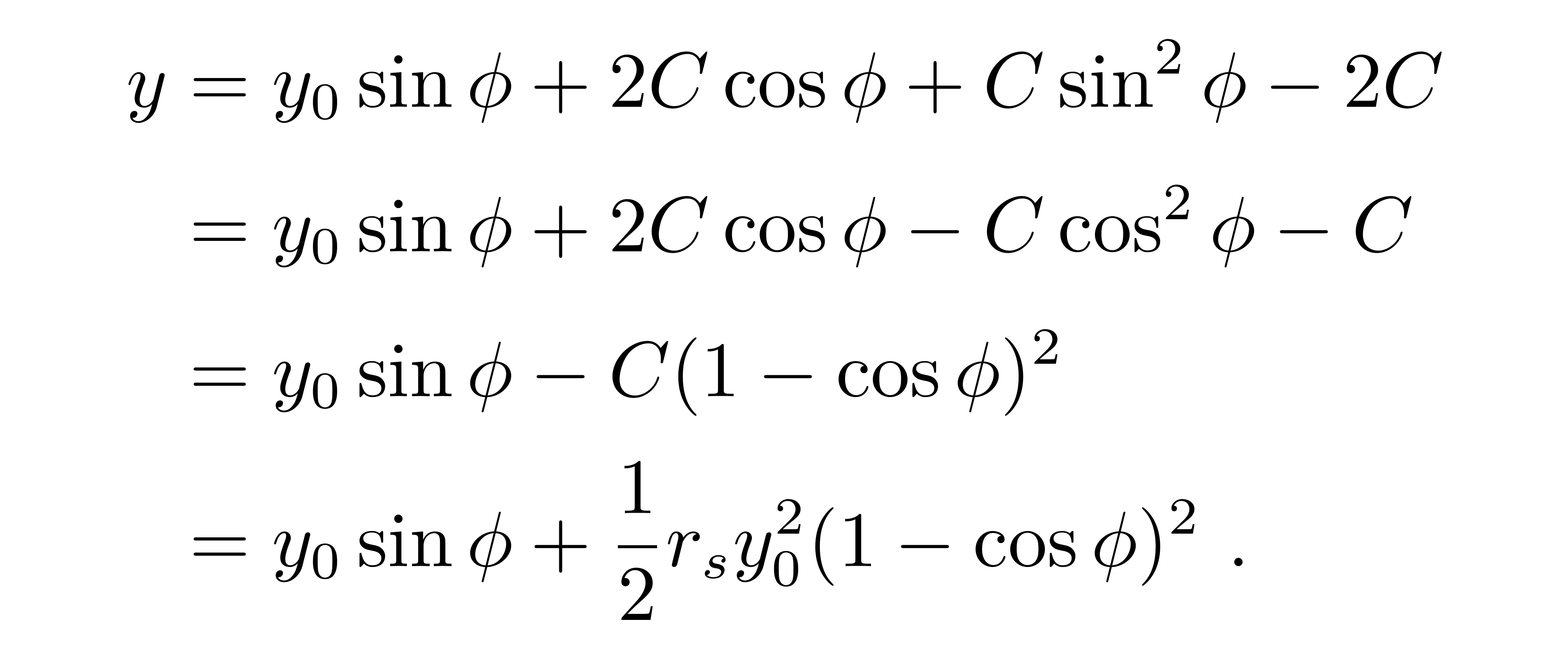
可以看到第二项是一个完全平方项，所以多了第二项后，y比牛顿引力的情况更大了。一方面，在Φ→0处仍然有y→0的极限，这意味着Φ必须偏离π的取值，也就是光线出现了偏折。

在导出B+D=0这一关系时，已经蕴含了光线在Φ→0的角度入射这一条件。光的出射角一定只有一个小的偏差，因此就可以在零级近似出射角π的基础上加上一个偏折角δ，记为Φ→π+δ，那么有

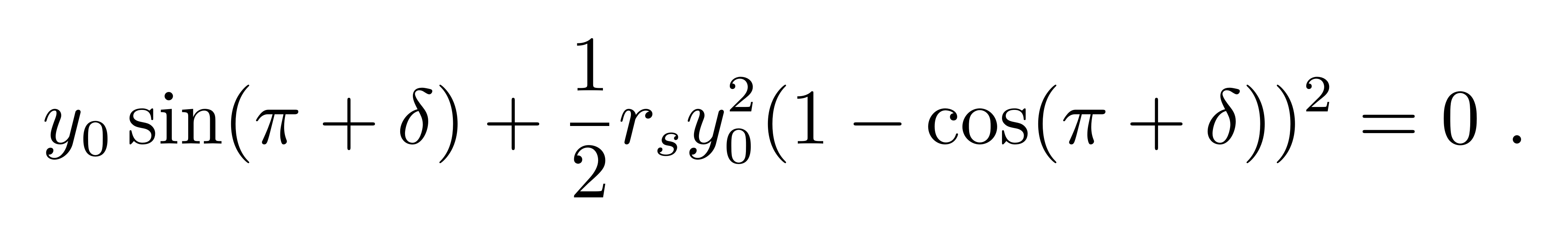
取δ的小角近似，并约掉一个y_0，

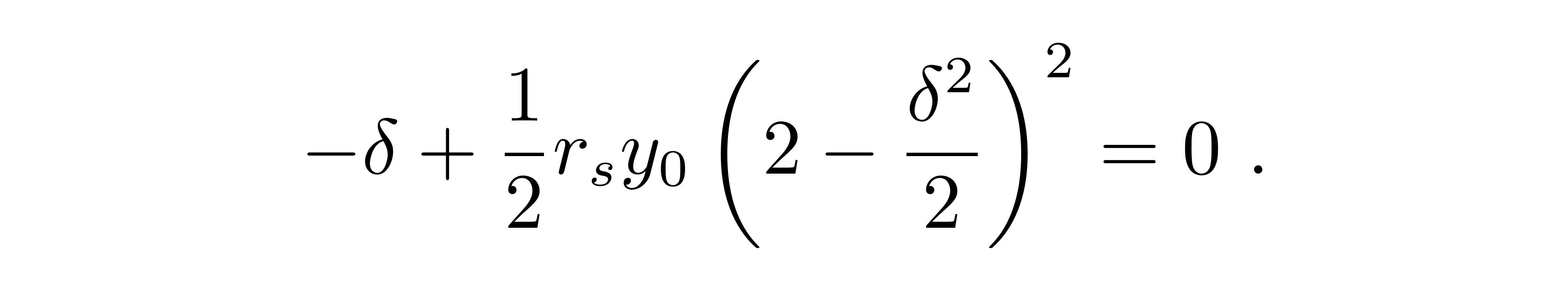
进一步地，由于r_sy_0=r_s/r_0是一个和δ同阶的一阶小量，所以对于(2-δ²/2)²只需要保留到零阶，这样就得到

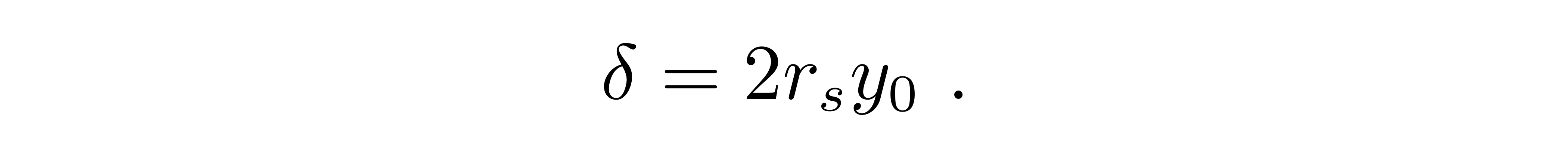
这里需要额外补充一下对参数A的讨论。在零级近似解中，y_0代表轨迹离引力源最近距离的倒数。对于一级近似解，试探函数依然是在π/2附近取到y的极大值，也就是r的极小值，所以依然可以近似认为

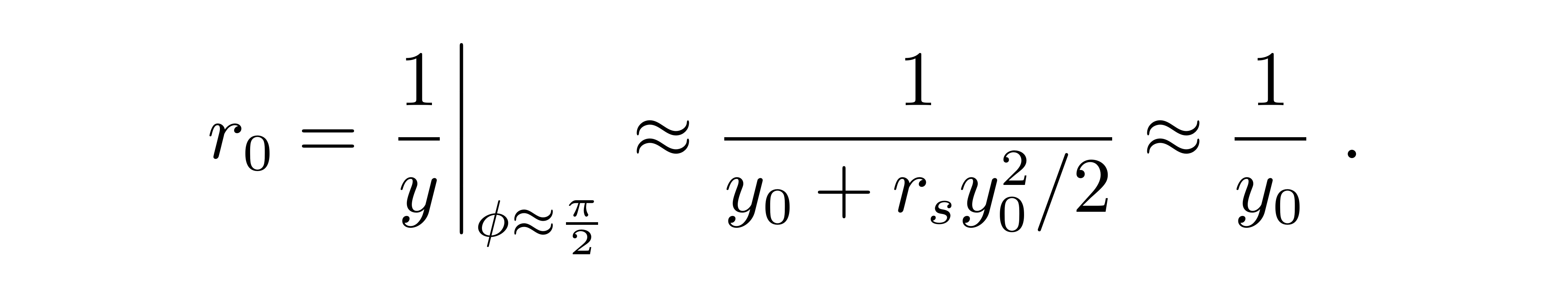
于是，偏折角就可以写成

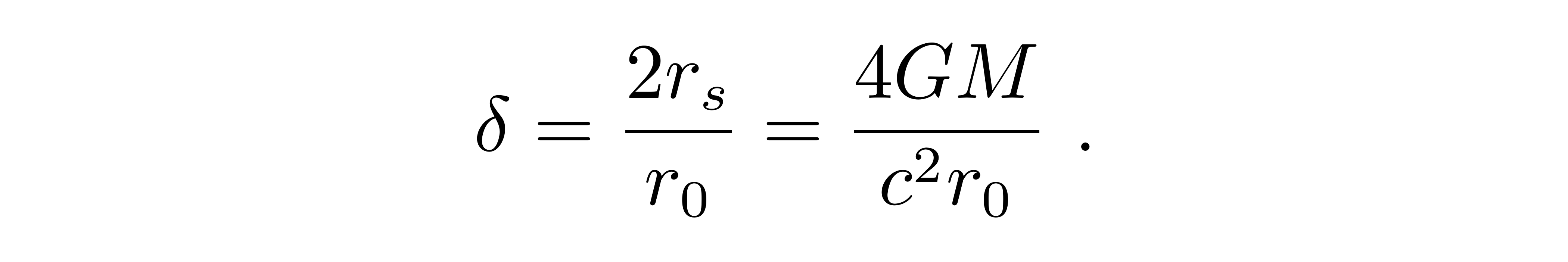
这个结果和用等效折射率的方法所得到的结果一致。相比于经典牛顿引力的结论，广义相对论对光线偏折的预言是其整整两倍，带入真实数据得到结果是1.75角秒，这与爱丁顿团队观测日全食得到的星光偏移数据更加吻合，从而有力地证明了广义相对论的正确性。

对于微扰解法的局限性在这里需要一些讨论。当引力场极端强大时（例如靠近黑洞视界附近），微扰近似将完全失效。从方程上来看，就是当星体的史瓦西半径可以和光路距离星体的距离相比时，微扰方法将不能使用。在这种情形下，时空曲率极高，无法看作平直空间的小扰动；高阶项的贡献显著甚至主导，必须使用完整的施瓦西度规进行精确计算。黑洞周围典型的极端情形之一便是光子球（Photon Sphere）。

光子球对应于黑洞周围特定的稳定或非稳定圆形光子轨道，光线可以围绕黑洞“环绕”多圈甚至无限圈。在光子球附近，微扰方法的条件（即扰动项远小于背景度规项）明显被破坏，因而必须转向完整的非线性精确解来描述光线轨迹。从这个角度看，黑洞光子球的存在恰好体现了微扰方法适用性的一种边界和极限，体现了广义相对论在不同引力尺度上的丰富内涵。

（张朝阳计算光线偏折角）

据了解，《张朝阳的物理课》于每周周日中午12时在搜狐视频直播，网友可以在搜狐视频APP“关注流”中搜索“张朝阳”，观看直播及往期完整视频回放；关注“张朝阳的物理课”账号，查看课程中的“知识点”短视频；此外，还可以在搜狐新闻APP的“搜狐科技”账号上，阅览每期物理课程的详细文章。